Calculations

We are hunting for peptides that may have taken up heavy atom isotopes such as ¹⁵N. Since there can be anywhere from 0 to maxIso uptake of heavy atoms we need to search for a range of mz's for each peptide.

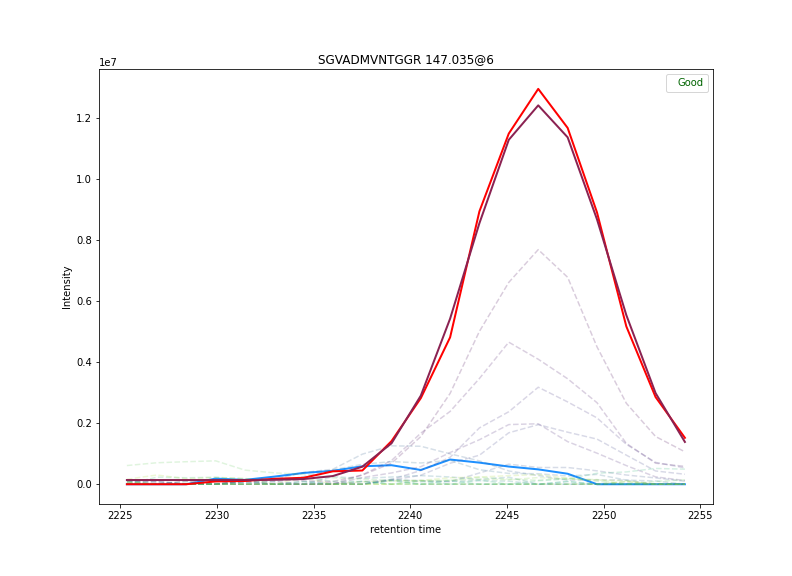
We try and fit a gaussian to the intensities of the peptide without isotopic enrichment

$$\begin{equation} \text{monoFitParams} \equiv \text{minimize}[\mu,\sigma, k, b] = \sum_i \left(k \times e^{-( \text{retention-time}_i - \mu)^2/2 \sigma^2} + b - \text{intensity}^{o}_i \right)^2 \end{equation}$$

where $`\text{intensity}^{o}_{i}`$ are the intensities found for the peptide with no isotopic enrichment. (Actually we fit to a smoothed version of the intensities)

We use quadrature to estimate the area under this curve.

$$\begin{equation} A_{\text{o}} = \int_{l_b=\max(\mu_{opt} - 2 * \sigma_{opt} , rt_0)}^{u_b=\min(\mu_{opt} + 2 * \sigma_{opt} , rt_n)} d\text{rt} \left( k_{opt} \times e^{-(\text{rt} - \mu_{opt})^2/2 \sigma_{opt}^2}+ b_{opt} \right) \end{equation}$$

which we can do analytically as: $$\begin{equation} A_o = \text{b}_\text{opt} \times (u_b - l_b) + k_\text{opt} \times \sigma_\text{opt}\times \sqrt{\frac{\pi}{2}} \left[\text{erf}\left(\frac{1}{\sqrt{2}}\frac{u_b - \mu_\text{opt}}{\sigma_\text{opt}}\right) - \text{erf}\left(\frac{1}{\sqrt{2}}\frac{l_b - \mu_\text{opt}}{\sigma_\text{opt}}\right) \right] \end{equation}$$

$`A_o`$ is stored as monoPeakArea.

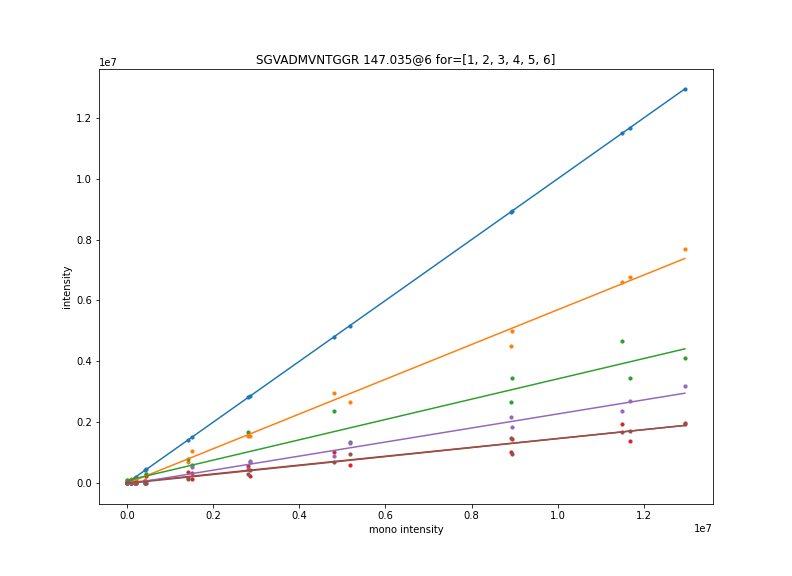
Estimating intensities of EICs

We now linearly fit the scatter plots of the heavy peptides with the base peptide. (with the configuration variable WITH_ORIGIN as False — the default — $`\alpha`$ is held to zero.)

$$\begin{equation} I^{\text{[eic]}}_{rt} \sim \alpha^{\text{[eic]}} + \beta^{\text{[eic]}} I^{\text{mono}}_{rt} \end{equation}$$

Note that the first value of isotopeEnvelopes is based on an mz that has negative enrichment (at least theorectically!) as a check. (See the blue line in the plot at top.)

If we integrate this relationship on both sides over the retention time range we get an intensity relationship:

$$\begin{equation} \text{isotopeEnvelopes[eic]} = A^{\text{[eic]}} = \max(0, \alpha^{\text{[eic]}} \times( u_b - l_b) + A_{\text{o}} \times \beta^{\text{[eic]}}) \end{equation}$$

$`\alpha`$ is probably small due to the fact that there will be zero intensities on both sides at the margins.

---

Isotopic Abundance

The isotopic abundance of a peptide is calcualated from Efficient Calculation of Exact Fine Structure Isotope Patterns via the Multidimensional Fourier Transform (2014) by Andreas Ipsen.

We use this a lot since we need to calculate it with elevated abundance levels for the isotope we are using in our experiment. We use the notation $`\text{ndist}_i^{E}`$ to identify the abundances found if the environmental abundance (of our heavy isotope is E).

We calculate isotopic abundance from natural abundance to (user specified) maximum labelled abundance

$$\begin{equation} a_i^\text{iso} = \text{natural-abundance} + \frac{i}{N}\times(\text{maximumLabelEnrichment} - \text{natural-abundance}) \quad\forall\; i \in [0,N] \end{equation}$$

where N is taken to be the labelled element count of the peptide. Then we adjust abundances of the labelled element (so they always sum to 1)

$$\begin{equation} \text{adjustedAbundance}_{k} = \left\{ \begin{array}{ll} (1-a^\text{iso}) \times \frac{\text{Abundance}_k}{\sum_{l\ne \text{iso}} \text{Abundance}_l} & \text{if}\; \text{iso} \ne k \\ a^\text{iso}\; & \text{if}\; \text{iso} = k\end{array}\right. \end{equation}$$

for each of these values we recalulate the ndist array with these new abundances.

$$\begin{equation} \begin{array}{cc} & \begin{array}{ccc} \quad a_o & a_1 & \cdots & a_N \\ \end{array} \\ \begin{array}{r c c} \text{iso}_0 \\ \text{iso}_1 \\ \text{iso}_2 \\ \cdots \\ \text{iso}_{\text{isoMax}} \end{array} & \left[ \begin{array}{c c c} \left[\begin{array}{c} \color{red}{n} \\ \color{red}{d} \\ \color{red}{i} \\ \color{red}{s} \\ \color{red}{t} \end{array} \right] \left[\begin{array}{c} \color{green}{n} \\ \color{green}{d} \\ \color{green}{i} \\ \color{green}{s} \\ \color{green}{t} \end{array} \right] \;\cdots\; \left[\begin{array}{c} \color{blue}{n} \\ \color{blue}{d} \\ \color{blue}{i} \\ \color{blue}{s} \\ \color{blue}{t} \end{array} \right] \end{array} \right] \end{array} \begin{array}{c} \; \\ \times \mathbf{w} \end{array} \begin{array}{c} \; \\ \quad = \end{array} \begin{array}{c} \; \\ \quad \mathbf{A} \times \mathbf{w} \end{array} \begin{array}{c} \; \\ \quad \sim \end{array} \begin{array}{c} \; \\ \quad \mathbf{I}^{exp} \end{array} \end{equation}$$

With $`\mathbf{w} \ge 0`$ and $`\text{labelledEnvelopes} \equiv \mathbf{w}`$. We do a Non-Negative Least Squares (NNLS) optimisation to estimate the $`\mathbf{\hat{w}}`$.

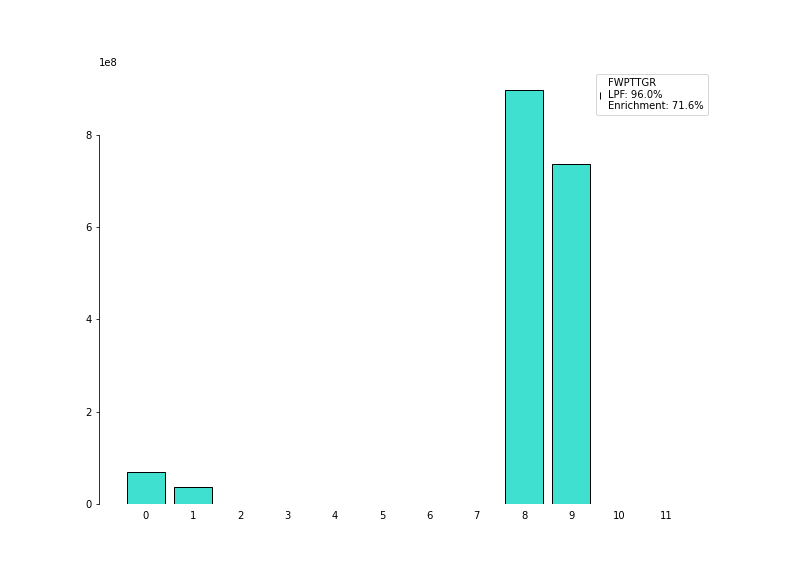
We calcuate a scaled deviance as a measure of goodness of fit.

$$\begin{equation} \frac{\sqrt{\Vert \mathbf{A} \times \mathbf{\hat{w}} - \mathbf{I}^{exp} \Vert^2}}{\sum_i \hat{w}_i } \end{equation}$$

If we turn the positive weights $`\mathbf{\hat{w}}`$ into fractions $`f_i = w_i / \sum_{i=0}^{N} w_i`$ then LPF $`\equiv \text{relativeIsotopeAbundance}`$ (an estimate of the fraction of this peptide that include some/any heavy atoms) $$\begin{equation} \text{relativeIsotopeAbundance} = 1 - f_0 = \sum_{i=1}^N f_i \end{equation}$$

enrichment is an estimate/average of the fraction of heavy atoms (of the labelled type) in the peptide:

$$\begin{equation} \text{enrichment} = \langle a_i^{iso} \rangle = \sum_{i=0}^N f_i a_i^{iso} \ge 0 \end{equation}$$

where $`N`$ is the labelled element count of the peptide. With this $`\text{enrichment}`$ we recalulate $`\text{ndist[enrichment]}`$ using this abundance of the isotope. Then we calculate the Pearson correlation coefficient: with $`x = \text{heavyDistribution}`$ and $`y = \text{ndist[enrichment]} \equiv \text{ndist}^E`$

$$\begin{equation} \text{heavyCor} = r = \frac{\sum (x - \bar{x}) (y - \bar{y})} {\sqrt{\sum (x - \bar{x})^2 \sum (y - \bar{y})^2}} \end{equation}$$

$`\text{heavyDistribution}`$ is just a "normalized" version of $`\text{isotopeEnvelopes}`$: $$\begin{equation} \text{heavyDistribution} = \max(0, \text{isotopeEnvelopes} - A_o \frac{\text{ndist}}{\text{ndist[0]}}) \end{equation}$$

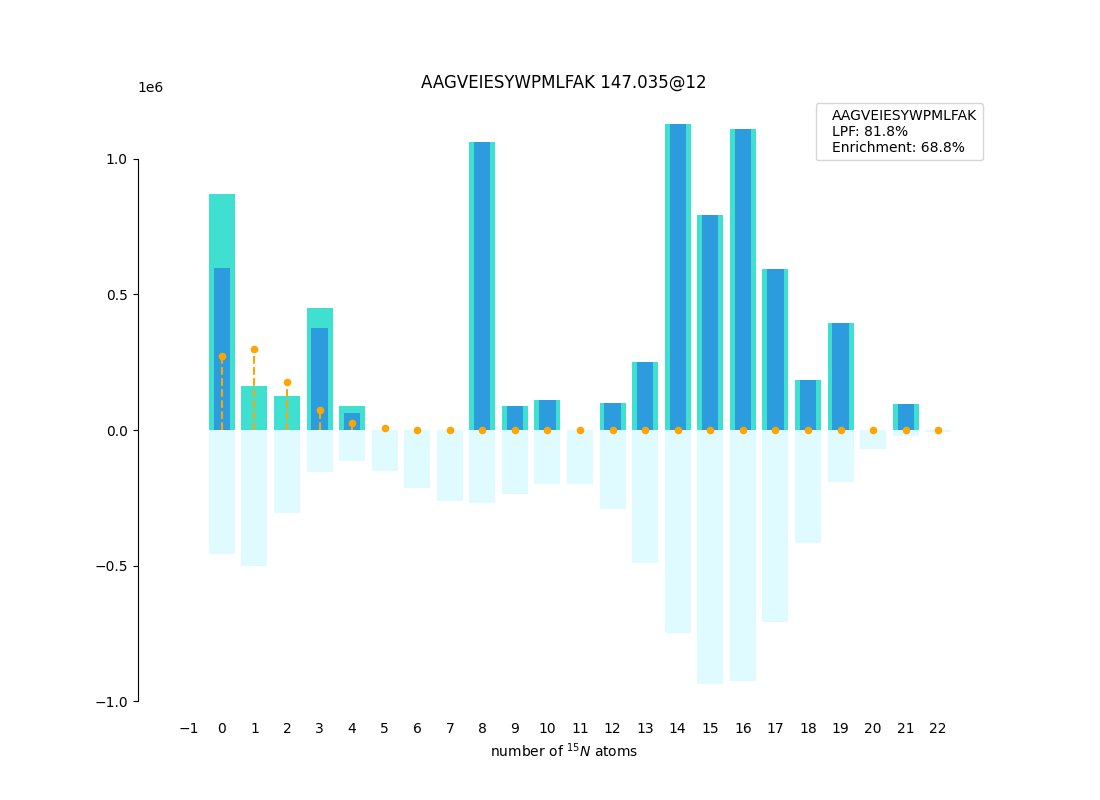
Fitted Envelopes Plot

With E as enrichment and relativeIsotopeAbundance as LPF we calculate : $$\begin{equation} \text{theoreticalDist} = \mathbf{A} \times \mathbf{\hat{w}} \end{equation}$$

• naturalDist $`A_o \times \text{ndist}`$ is plotted as orange vertical dashed lines.
• theoreticalDist is mirrored on the x-axis and plotted inverted as .
• $`\text{heavyDistribution} = \max(0, \text{isotopeEnvelopes} - \text{naturalDist})`$ is plotted as
• isotopeEnvelopes is plotted as
• the negative enrichment value is used to filter hits $`\frac{\text{isotopeEnvelopes}[0]}{\text{isotopeEnvelopes}[-1]} \ge \text{monoMinus1MinRatio}`$